FrontierMath: Revealing the True Limits of AI Mathematical Reasoning

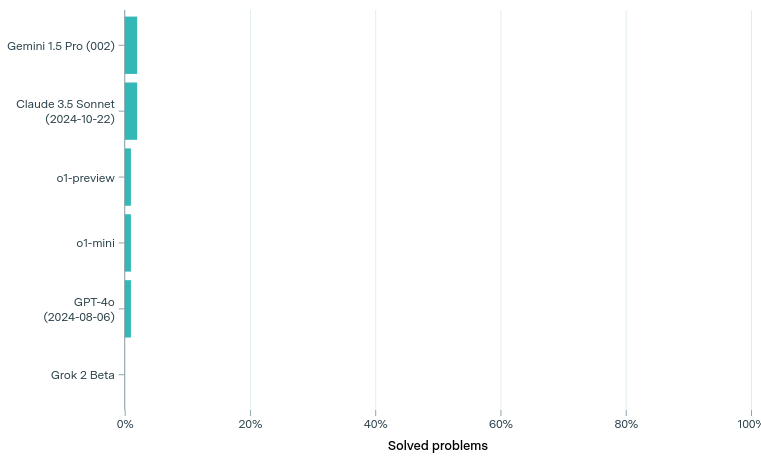
A groundbreaking mathematical benchmark developed by Epoch AI, in collaboration with over 60 leading mathematicians, has exposed significant limitations in current AI systems’ ability to solve complex mathematical problems. Despite achieving over 90% success rates on traditional tests, leading AI models including GPT-4, Claude 3.5, and Gemini 1.5 Pro solve less than 2% of these expert-level problems. This comprehensive evaluation system features original, unpublished problems spanning multiple mathematical disciplines, establishing new standards for measuring AI capabilities in advanced reasoning and creative problem-solving. The findings reveal a critical gap between computational ability and genuine mathematical understanding, highlighting necessary directions for future AI development.
Development and Methodology
The benchmark, named FrontierMath ¹, was developed by Epoch AI, a non-profit AI research organization, in collaboration with over 60 leading mathematicians from prestigious institutions worldwide, including MIT, Harvard, and UC Berkeley. Epoch AI spearheaded the initiative, designing the overall framework and methodology, while the participating mathematicians contributed their expertise in crafting the challenging, original problems that form the core of the benchmark. This collaborative effort ensured a diverse and comprehensive set of mathematical challenges spanning multiple disciplines.
The full methodology and findings are detailed in the accompanying research paper, ‘FrontierMath: A Benchmark for Evaluating Advanced Mathematical Reasoning in AI’ ². The paper presents the rigorous development process, including the selection criteria for problems, the validation protocols established with the mathematical community, and detailed statistical analysis of model performance across different mathematical domains. The research also explores the theoretical foundations underlying the benchmark’s design and discusses its implications for future AI development. Interested readers can access the complete research report and technical specifications at arXiv ².
Unlike traditional benchmarks, FrontierMath features entirely original, unpublished problems that require hours or days for expert mathematicians to solve. The problem set spans multiple disciplines, from computational number theory to algebraic geometry, ensuring comprehensive testing of mathematical reasoning capabilities. This represents a significant advancement in AI evaluation methodology, providing a rigorous assessment of AI systems’ ability to tackle complex, real-world mathematical challenges.
The technical architecture implements rigorous anti-contamination measures and automated verification systems using Python and SymPy integration. This ensures objective evaluation and reproducible results while preventing the data contamination issues that have compromised previous benchmarks’ effectiveness.
To illustrate the level of complexity in FrontierMath problems, consider the following example ³:

This problem demonstrates the type of advanced reasoning and multi-step approach required, moving well beyond simple computation or pattern recognition.
Key Findings and Performance Metrics
The most striking revelation is the stark performance gap between AI systems’ capabilities on traditional versus advanced mathematical problems ³. While leading models excel at simpler benchmarks with 90%+ success rates, they achieve less than 2% success on these expert-level challenges. This dramatic difference highlights current AI limitations in complex reasoning and creative problem-solving.
As noted by Fields Medal winner Terence Tao, “These are extremely challenging… I think that in the near term basically the only way to solve them, short of having a real domain expert in the area, is by a combination of a semi-expert like a graduate student in a related field, maybe paired with some combination of a modern AI and lots of other algebra packages.” ³
The benchmark’s strikingly low success rates have generated enthusiastic response from the AI research community. Noam Brown of OpenAI notably remarked, on X ‘I love seeing a new eval with such low pass rates for frontier models. It feels like waking up to a fresh blanket of snow outside, completely untouched.’ ³ This poetic metaphor captures the excitement among researchers about having a new, unsolved challenge that represents genuine room for improvement. Unlike many AI benchmarks that quickly become obsolete as models achieve near-perfect scores, FrontierMath’s sub-2% success rate presents a vast unexplored territory for advancement in AI capabilities. This ‘untouched snow’ represents both the current limitations of AI systems and the extensive opportunities for fundamental breakthroughs in mathematical reasoning.
Quality Assurance and Validation
The benchmark underwent extensive peer review to ensure problem correctness and clarity, maintaining an approximately 5% error rate during the review phase – comparable to other major machine learning benchmarks. Problems are designed to be “guessproof” through complex numerical answers or mathematical objects as solutions, ensuring less than 1% chance of correct random guesses ².
The validation process included endorsement from multiple Fields Medal winners and leading mathematicians, confirming the exceptional difficulty level and appropriateness of the problems for evaluating advanced mathematical reasoning capabilities.
Implications for AI Development
The findings provide clear metrics for measuring progress in AI’s mathematical capabilities and identify specific areas requiring improvement. The significant performance gap demonstrates the need for fundamental advances in AI’s ability to perform creative problem-solving and complex reasoning, beyond mere pattern recognition and computational processing.
The benchmark’s results suggest that current AI systems, while powerful in specific domains, remain far from achieving human-like mathematical understanding and creativity. This insight is particularly valuable for directing future research and development efforts in AI technology.
Future Directions and Implementation
Ongoing development plans include expanding the problem set while maintaining rigorous standards and conducting regular evaluations of AI models against the benchmark. The initiative also includes plans to release sample problems to help researchers better understand and prepare for the challenges presented.
The broader impact extends beyond pure mathematics into potential applications in automated theorem proving and advanced problem-solving across various scientific domains. This comprehensive evaluation system sets new standards for measuring and advancing AI capabilities in complex reasoning tasks.
Conclusion
The benchmark represents a significant milestone in AI evaluation, providing unprecedented insight into current technological limitations and future development needs. Its rigorous methodology and comprehensive scope establish new standards for measuring AI capabilities in advanced mathematical reasoning. The stark performance gap revealed between traditional and expert-level problems underscores the significant work still required to achieve human-like mathematical understanding in AI systems.
These findings have important implications for both the academic and industrial AI communities, suggesting the need for fundamental advances in how AI systems approach complex reasoning and creative problem-solving tasks. As development continues, this benchmark will serve as a crucial tool for measuring progress toward more sophisticated AI mathematical capabilities.
Sources: